Robotnačka-03
Zo stránky SensorWiki
Úloha 3: Kolieska
Vypočítajte a overte, aké majú byť rýchlosti koliesok, aby robot nakreslil kružnicu s polomerom 10 cm
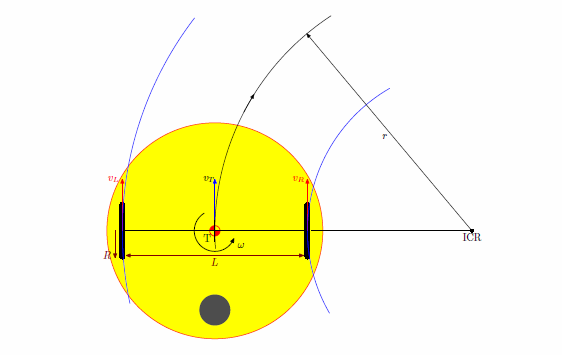
Robot sa v prípade nerovnakých rýchlostí koliesok bude stáčať na tú stranu, kde má pomalšie koliesko. Tento pohyb možno charakterizovať ako pohyb po oblúku okolo tzv. okamžitého stredu otáčania (ICR - Instantaneous Center of Rotation), pričom polomer tohto oblúka označíme r. Pokiaľ označíme symbolmi Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v_L}
rýchlosť ľavého a
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v_R}
rýchlosť pravého kolesa, pre polomer otáčania okolo ICR platí
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r = \frac{L}{2} \frac{v_R + v_L}{v_R - v_L} \qquad \mbox{(8. 2)}}
Pre okamžitú tangenciálnu rýchlosť stredu vozíka T platí:
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v_T = \frac{v_R + v_L}{2} \qquad \mbox{(8. 3)} }
A pre a uhlovú rýchlosť otáčania vozíka okolo ICR platí:
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \omega_T = \frac{v_R - v_L}{L} \qquad \mbox{(8. 4)} }
Ak uvedené vzťahy nebudeme odvodzovať, ale ich prevezmeme z prednášok, môžeme si aspoň overiť ich platnosť na základe toho, čo vieme z predošlých dvoch úloh. Aký je polomer r otáčania, ak sa obe hnacie kolesá otáčajú rovnakou uhlovou rýchlosťou v rovnakom smere, a ako je to ak sa otáčajú v opačnom smere?
Vypočítané hodnoty vyskúšajte a overte. Odmerajte priemer nakreslenej kružnice (Ako sa meria priemer kružnice?). Dosiahli ste výsledok s uspokojivou presnosťou? Ak nie, čo je na príčine a ako by ste ho zlepšili?
Poznámka:
Pri rýchlostných príkazoch je koliesko roztočené požadovanou rýchlosťou okamžite, čím sa pri vyšších rýchlostiach môže vyskytnúť tzv. strácanie kroku. Polohové príkazy, pri ktorých predpokladáme vyššie požiadavky na presnosť sú ošetrené tak, že rozbiehanie aj spomaľovanie je realizované lichobežníkovým rýchlostným profilom.