Zaciatok
Zo stránky SensorWiki
História
Predhistória
Počítanie a počítače sú úzko prepojené s číslami a číselnými sústavami. Donedávna sa v Európe používali rímske číslice. Napr. číselná sústava používaná v Babylone (1900 to 180
- 1969 - first computer networks
- 1970 – UNIX
- 1971 - First true microprocessor (Intel)
- 1965 Objavená bola aj myš, ale začala sa používať až 1985.
Zobrazenie informácií v počítači
xxxxxxxxxxxxxxx
Číselné sústavy
Delíme ich na :
- polyadické (pozičné) číselné sústavy PČS, ktoré môžeme rozvinúť do mocninového radu
- nepolyadické (nepozičné)číselné sústavy NČS. Napr.: rímska číselná sústava (IX, X, XIV)
Zobrazenie informácií v počítači
Počítanie a počítače sú úzko prepojené s číslami a číselnými sústavami. V bežnom živote používame dekadické čísla (číslice 0,1,2,2,3,4,5,6,7,8,9)v pozičnej číselnej sústave. Napr.: Moderné počítače vnútorne pracujú s binárnymi číslami=dvojkovými(číslice 0 a 1). Napr.:
,
,
,
,
Vlastnosti PČS:
- Maximálne zobraziteľné číslo:
pre celé čísla: pre desatinné čísla:
- Minimálne číslo v absolútnej hodnote rôzne od nuly:
- Krok diskrétnosti:
- Kapacita číselnej sústavy pre m-rádové čísla: Pr.: z = 10, m = 3, K = 1000 možných čísiel (0..999)
- Počet zobrazujúcich rádov:.
- Desetinná čiarka, bodka si vo všetkých číselných sústavách odpovedá. Samostatne môžeme prevádzať obe časti(celu i zlomkovú).
Napríklad dekadické číslo môžeme rozpísať do tvaru
hodnoty číslic sú .
Pozičné číselné sústavy (PČS)
Hodnotu celého nezáporného čísla vyjadríme v tvare polynómu:
,
kde
- z je základ pozičnej sústavy z ≥ 2 (2, 8, 10, 16)
- číslice ( 0 ≤ < ) ak je prirodzené číslo, potom
Poloha číslice určuje rád číslice, ktorý je definovaný váhou , jerád sústavy. Ak potrebujeme zapisáť racionálne číslo (väčšina) použijeme záporné mocniny až do rádu
Bežne používame skrátený zápis racionálneho čísla
Poznámka: Rozšírenie na záporné čísla použitím znamienka mínus (-) pred číslom a používanie desatinnej čiarky je vhodné pre ľudí. V žiadnom prípade to nie je vhodný zápis pre počítač.
Pre:
získame dvojkovú - binárnu číselnú sústavu (0,1)
získame osmičkovú - oktálovú číselnú sústavu (0,1,2,...,7)
získame desiatkovú - dekadickú číselnú sústavu (0,1,2,...,9)
získame šesťnástkovú - hexadecimálnu číselnú sústavu (0,1,2,...,9,A,B,C,D,E,F). Slovo hexadecimálny pochádza z gréckeho (hexi - šesť) a latinského (decem - desať).
Vlož tabuľku.
Vlastnosti PČS:
1. Maximálne zobraziteľné číslo:
Pozičné číselné sústavy – prevody
Prevod z desiatovej sústavy do číselnej sústavy so základom :
Prevod sa vykonáva zvlášť pre celočíselnú časť čísla a zvlášť predesatinnú časť čísla
Prevod celočíselného dekadického čísla do sústavy so základom :
Metóda je založená na postupnom celočíselnom delení dekadického , číslom ,. Celočíselné delenie:
,
Kde: - delenec, - deliteľ , – podiel a - zvyšok, sú celé čísla.
,
. Príklad: Prevod do 8-ovej sústavy:

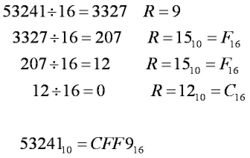
Príklad: Prevod do binárnej sústay

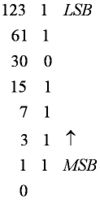
Počítanie a počítače sú úzko prepojené s číslami a číselnými sústavami. Donedávna sa v Európe používali rímske číslice. Napr. číselná sústava používaná v Babylone (1900 to 180
Vlož obrázok.
Nepozičné číselné sústavy:
V nepozičných číselných sústavách vždy neplatí: .
Rímska číselná sústava (najznámejšia nepolyadická sústava).
Skladá sa zo 7 symbolov: I V X L C D M.
I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000.
Zápis: Sprava doľava. Výnimka: Ak zapíšeme číslice I, X, C pred väčšiu číslicu, potom menšiu od väčšej odčítame.
Napr: MMXMIV = 1000 + 1000 + (1000 - 10) + (5 - 1) = 2994
Číslice V, L, D môžu byť zapísané len raz a číslice I, X, C najviac trikrát za sebou. M sa môže opakovať ľubovoľne krát.
Príklad: Číslo zobrazené v rímskej číselnej sústave je zapísané ako číslo CCXV, kde jednotlivé znaky odpovedajú hodnotám .















![{\displaystyle [2]_{3}=2000,[3]_{2}=300,[4]_{1}=40,[3]_{-1}=0,3,[7]_{-2}=0,07}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a95ca407211a84850b2af1fb1e5fd30d70dffeb3)























![{\displaystyle [a_{i}]_{i}=(a_{i})z^{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c96dc25dbb542482c36e80ad8bd1d6eb50d3ae95)

![{\displaystyle [(C)]_{3}=100,[(C)]_{2}=100,[(X)]_{1}=10,[(V)]_{0}=5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a11cf513e6d3d1b1cb0664a261440247f35da484)