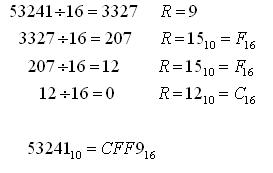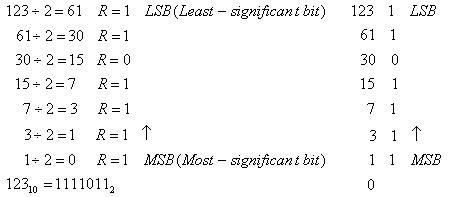Prevody medzi číselnými sústavami
Zo stránky SensorWiki
Teoretický úvod
Podrobnejší popis a teóriu nájdete na stránke Číselné sústavy
Príklad 1: Preveďte číslo 5324110 do hexadecimálnej (šestnástkovej) sústavy.
Príklad 2: Preveďte číslo 12310 do binárnej (dvojkovej) sústavy.
Príklad 3: Záporné čísla
Priamy kód -- jeden bit (MSB) je vyhradený pre znamienko
0 000 0 0 001 1 0 010 2 0 011 3 0 100 4 0 101 5 0 110 6 0 111 7 1 000 -0 1 001 -1 1 010 -2 1 011 -3 1 100 -4 1 101 -5 1 110 -6 1 111 -7
3 + (-3) = 0011 + 1011 = 1110 = -6 nOK 5 + (-3) = 0101 + 1011 = 1 0000 = 0 nOK
Inverzný kód -- podobne ako priamy, MSB je znamienko
0 000 0 0 001 1 0 010 2 0 011 3 0 100 4 0 101 5 0 110 6 0 111 7 1 000 -7 1 001 -6 1 010 -5 1 011 -4 1 100 -3 1 101 -2 1 110 -1 1 111 -0 3 + (-3) = 0011 + 1100 = 1111 = -0 OK 5 + (-3) = 0101 + 1100 = 1 0001 = 1 nOK
Je nutná korekcia: pripočítať CY bit k LSB 5 + (-3) = 0101 + 1100 = 1 0001 = 0001+1 = 0010 = 2 OK
Doplnkový kód -- inverzný kód + 1, stále platí MSB je znamienko ale naviac funguje aritmetika
0 000 0 0 001 1 0 010 2 0 011 3 0 100 4 0 101 5 0 110 6 0 111 7 1 111 -1 1 110 -2 1 101 -3 1 100 -4 1 011 -5 1 010 -6 1 001 -7 1 000 ?? => -8 3 + (-3) = 0011 + 1101 = 1 0000 = 0 OK 5 + (-3) = 0101 + 1101 = 1 0010 = 2 OK -7 + (-1) = 1001 + 1111 = 1 1000 = -8
Príklady na precvičovanie
Vyplňte nasledovnú tabuľku
| DEC | HEX | BIN |
|---|---|---|
| 0 | ||
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| 13 | ||
| 14 | ||
| 15 |
2. Preveďte niekoľko čísel z jednej sústavy do inej podľa pokynov cvičiaceho.
3. Rozsahy Bajt, 2Bajty, 4Bajty (min, max)
4. BCD kód
5. ASCII kód
6. Záporné čísla - doplnkový kód
Otestujte sa sami
TODO:
- http://www.rapidtables.com/convert/number/hex-dec-bin-converter.htm
- http://calc.50x.eu/
- https://www.mathsisfun.com/binary-decimal-hexadecimal-converter.html
- http://www.binaryhexconverter.com/
- https://www.algoritmy.net/article/80/Prevod-cisla-mezi-soustavami
Zložitejšie úlohy
1. Riešenie nasledovného problému vám pomôže ostať bdelými aj na zvyšku cvičenia. Preveďte do hexadecimálnej sústavy 12648430(dec).
2. Vysvetlite, prečo programátori oslavujú vianoce už v októbri OCT18 (pomôcka: preveďte 18 z osmičkovej do desiatkovej sústavy).
3. Pre adresovanie počítačov v siet internet sa používa IPv6 adresa, ktorá
pozostáva z 8 skupín štvorciferných hexadecimálnych číslic oddelených dvojbodkami, napríklad
2001:0db8:85a3:0000:0000:8a2e:0370:7334
Sledovaním sieťovej komunikácie na podozrivom počítači pomocou binárneho analyzátora sme zistili, že najčastejšie komunikuje s nasledovným serverom
0010 1010 0000 0011 : 0010 1000 1000 0000 : 0010 0001 0011 0000 : 1100 1111 0000 0101 : 1111 1010 1100 1110 : 1011 0000 0000 1100 : 0000 0000 0000 0000 : 0000 0000 0000 0000
Preveďte binárny tvar na hexadecimálny a pomocou služby https://ipinfo.io/ zistite, s kým vlastník počítača komunikoval.
4. V ktorej sústave je toto pravda?
a) 10 + 11 = 101 b) 10 + 11 = 21
5. Ak uvažujeme jeden bajt (8 bitov), aký rozsah čísel vieme reprezentovať? Ak najvyšší (siedmy) bit bude
znamienko (0 = +, 1 = -) aký bude rozsah? V doplnkovom kóde bude aký rozsah?
6. Aký je rozsah pre 32-bitové celé čísla (signed, unsigned)?
7. Bonus za 2 body pre prvé riešenie tejto úlohy:
Jedna z prvých expedícií na Mars tam našla zvyšky civilizácie. Z rozličných artefaktov a obrázkov, ktoré tam našli, si vedci odvodili, že tvory, ktoré tu žili mali podobu štvornohých bytostí s jedným chápadlom, ktoré sa na konci rozvetvovalo na nezistený počet "prstov." Po ďalších hľadaniach a čiastočnej analýze marťasnkého písma boli prieskumníci schopní preložiť marťanskú matematiku. Našli nasledujúcu rovnicu:
5x2 - 50x + 125 = 0
pri ktorej boli ako riešenia uvedené x = 5 a x = 8. Prvý výsledok sa zdá byť správny, ale druhý nie. Medzi vedcami bol aj jeden, ktorý našiel dôkazy o tom, že Marťania sa ku svojmu číselnému systému dostali postupne veľmi podobne ako aj my. Čo myslíte, koľko prstov mali Marťania? (Z Bent z Tau Beta Pi , Február 1956).