Robotnačka-03

Úloha 3: Kolieska

Vypočítajte a overte, aké majú byť rýchlosti koliesok, aby robot nakreslil kružnicu s polomerom 10 cm

<googlevideo>-8790202110921792379</googlevideo>

Obr. 3: Pohyb pri nerovnakých rýchlostiach.

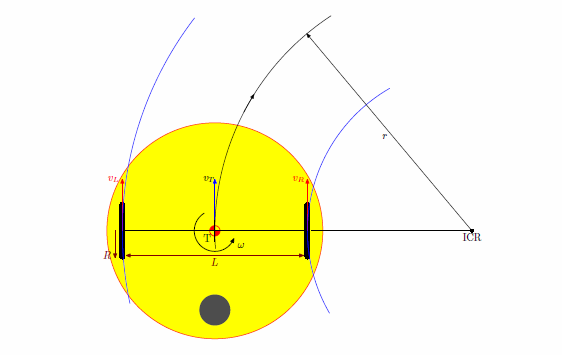
Robot sa v prípade nerovnakých rýchlostí koliesok bude stáčať na tú stranu, kde má pomalšie koliesko. Tento pohyb možno charakterizovať ako pohyb po oblúku okolo tzv. okamžitého stredu otáčania (ICR - Instantaneous Center of Rotation), pričom polomer tohto oblúka označíme r. Pokiaľ označíme symbolmi vL rýchlosť ľavého a vR rýchlosť pravého kolesa, pre polomer otáčania okolo ICR platí r = L 2 vR + vL vR − vL (8. 2) Pre okamžitú tangenciálnu rýchlosť stredu vozíka T platí: vT = vR + vL 2 (8. 3) A pre a uhlovú rýchlosť otáčania vozíka okolo ICR platí: !T = vR − vL L (8. 4) Ak uvedené vzťahy nebudeme odvodzovať, ale ich prevezmeme z prednášok, môžeme si aspoň overiť ich platnosť na základe toho, čo vieme z predošlých dvoch úloh. Aký je polomer r otáčania, ak sa obe hnacie kolesá otáčajú rovnakou uhlovou rýchlosťou v rovnakom smere, a ako je to ak sa otáčajú v opačnom smere? Robot sa bude pohybovať po priamke vtedy, keď sa obe kolieska budú otáčať súčasne rovnakým smerom. Keďže viete, že Robotnačka je poháňaná krokovými motormi, viete z katalógového listu motora určiť, koľko krokov je potrebných na jednu úplnú otáčku. Keď si posuvným meradlom zmeriate priemer kolieska, budete vedieť aj to, akú dráhu pri tejto úplnej otáčke Robotnačka prejde. No a potom už bude hračka vypočítať počet impulzov, aby dráha bola 10cm.

Vypočítanú hodnotu overte. Podarilo sa?

Pozor: Všimnite si závislosť na rozmeroch kolieska. V prípade zmeny rozmerov, nepresného zmerania, starnutia materiálu a pod. sa chyba zväčší.

Otázky: Dokážete úlohu splniť presne? Aká je teoretická chyba v mm? (pomôcka: vyjde vám pri delení celé číslo?) Aký je vplyv povrchu na riešenie úlohy? Čo sa stane, ak koliesko bude prešmykovať? Overte to tak, že nakreslíte niekoľkokrát za sebou štvorec a zistite, ako sa postupne zväčšuje odchýlka od koncového bodu.