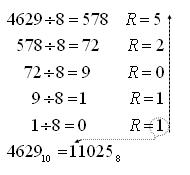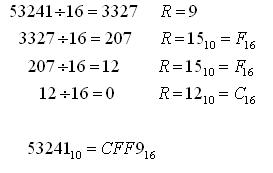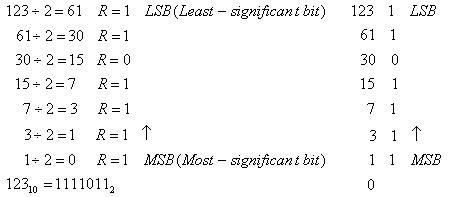Zaciatok: Rozdiel medzi revíziami
Zo stránky SensorWiki
| (173 medziľahlých úprav od 2 ďalších používateľov nie je zobrazených) | |||
| Riadok 1: | Riadok 1: | ||
== | == Základné stavebné prvky počítača == | ||
Počítač na spodnej úrovni pracuje ako elektronické zariadenie vytvorené z tranzistorov. | |||
Základný režim činnosti tranzistora je: Spínací režim. Tento môžeme z fyzikálnej podstaty popísať ako: Tranzistor prúd vedie, resp. nevedie. Jednotlivým stavom tranzistora môžeme priradiť logické úrovne odpovedajúce dvojkovej číslici (bit), označené ako log.0 a log.1. | |||
=== Tranzistor === | |||
* | Je všeobecné známe, že základom integrovaných obvodov je tranzistor. Podľa typu nosiča náboja ich delíme na: | ||
* | * bipolárne (dva typy nosiča - elektróny a diery) a | ||
* unipolárne (jeden typ nosiča). | |||
'''Unipolárna technológia výroby''': Sú to vlastne elektrickým poľom riadené tranzistory (FET – Field Effect Transistor). | |||
Historicky najstaršou technológiou je PMOS (Metal Oxid Semiconductor), ktorá používa unipolárny tranzistor s kanálom '''P'''. Vzhľadom na nízku rýchlosť a zlú zlučiteľnosť s TTL obvodmi sa nahradila technológiou NMOS (MOS tranzistor s kanálom '''N'''). Dosahuje vyššie rýchlosti, pretože elektróny sa pohybujú rýchlejšie ako diery. Výhodou je aj dobrá zlučiteľnosť s obvodmi TTL. Hradlo typu NMOS v invertujúcom zapojení používa ako záťaž spínacieho prvku rezistor. Hradlo NMOS zapojené ako invertor používa rezistor vo funkcii záťaže spínacieho obvodu. | |||
[[Obrázok:Tran_invertor.jpg]] | |||
xxxxxxxxxxx | |||
Výhody: | Výhody: | ||
*minimalizované straty | *minimalizované straty | ||
*zlučiteľné s TTL | *zlučiteľné s TTL | ||
=== | xxxxxxxxxxx | ||
=== Technológie CMOS (Complemntary MOS) === | |||
<math> | Dnes sa presadzujú technológie, v ktorých je rezistor nahradený „aktívnou“ záťažou - tranzistorom PMOS. Výhodou tejto technológie je eliminovanie stratového výkonu v statickom režime, kedy je jeden tranzistor vždy zatvorený. Tento obrázok je základom technológie CMOS (Complemntary Metal – Oxid Semiconductor). V tejto technológii <math>\ log.0</math> odpovedá napätie napätie <math>\ 0V</math> až <math>0\ 0,3V_{DD}</math> a <math>\ log.1</math> napätie <math>\ 0,7V_{DD} až </math> <math>\ V_{DD}</math>. Pre napájacie napätie <math>\ V_{DD}\ =\ 5,0V</math>, odpovedajúce napájaniu TTL obvodov, sú rozsahy nasledovné: <math>\ log.0\ =\ 0V</math> až <math>\ 1,5V</math> a <math>\ log.1\ =\ 3,5V</math> až <math>\ 5.0V </math>. | ||
Okrem <math>\ V_{DD}=5.0V</math> sa používa aj <math>\ V_{DD}=3.3V</math> a <math>\ V_{DD}=2.9V</math> | |||
[[Obrázok:Tran_CMOS.jpg]] | |||
V ďalšom budeme uvažovať N a P MOS tranzistory ako jednoduché spínače. Napájacie napätie je unipolárne: <math>\ V_{DD}</math>. | |||
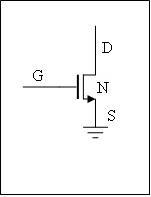
'''N-typ''' tranzistora má vývod '''S''' pripojený na ZEM. Aby bol tranzistor vodivý – '''ON''' musí byť napätie <math>\ U_{GS}</math> voči bodu '''S''' kladné. <math>\ U_{GS}</math> musí byť väčšie ako je minimálna prahová hodnota. Napr.: <math>\ U_{GS}\ = \ V_{DD}</math>. Prechod '''DS''' je potom vodivý. Ak je napätie <math>\ U_{GS}\ =\ 0V</math>, potom je tranzistor nevodivý – v stave '''OFF'''. | |||
[[Obrázok:N_typ.jpg]] | |||
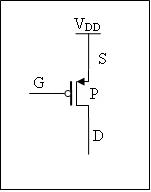
'''P-typ''' tranzistora má bod '''S''' pripojený na <math>\ V_{DD}</math>. Ak má byť tranzistor v stave '''ON''', musí byť napätie <math>\ U_{GS}</math> voči bodu '''S''' záporné. <math>\ U_{GS}</math> musí byť menšie ako je minimálna prahová hodnota. Napr.:<math>\ U_{GS}\ =\ 0V</math>. Ak je napätie <math>\ U_{GS}\ = \ V_{DD}</math>, potom je tranzistor nevodivý – v stave '''OFF'''. | |||
[[Obrázok:P_typ.jpg]] | |||
=== Logické úrovne – “ napätie“ === | |||
[[Obrázok:Log_urovne.jpg]] | |||
[[Obrázok:Log_urovne_cas.jpg]] | |||
[[Obrázok:Log_urovne_TTL.jpg]] | |||
== Zapojenie výstupov IC == | |||
[[Obrázok:Zap_out_IC.jpg]] | |||
== TTL obvody: logické úrovne == | |||
== Základné stavebné prvky počítačov sú vytvorené : == | |||
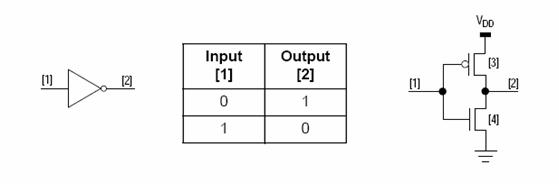
=== Invertor: === | |||
Obr. | |||
[[Obrázok:Invertor.jpg]] | |||
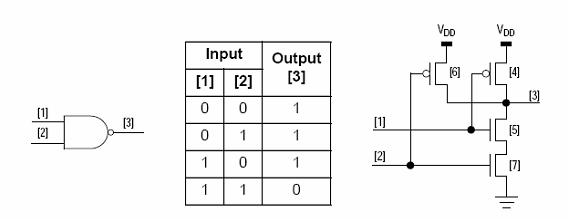
=== NAND: === | |||
[[Obrázok:NAND.jpg]] | |||
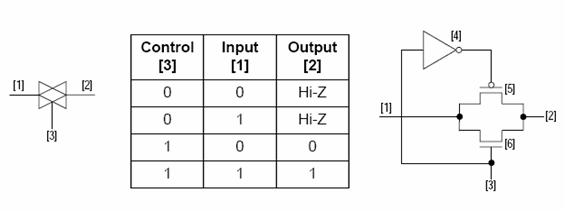
=== Spínač: === | |||
[[Obrázok:Spinac.jpg]] | |||
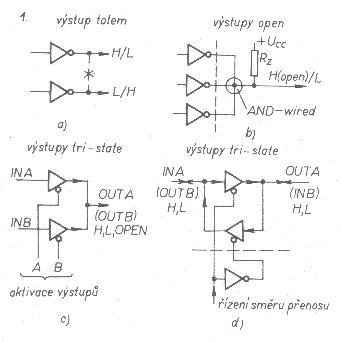
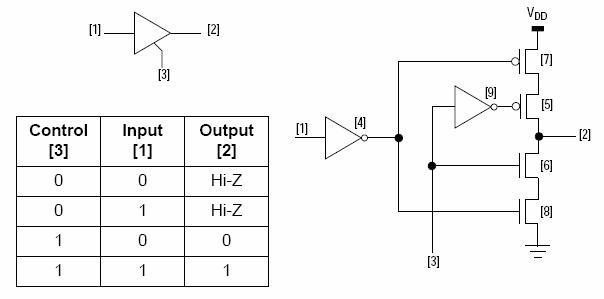
=== Trojstavový budič: === | |||
[[Obrázok:Trojstavbudic.jpg]] | |||
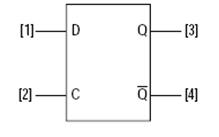
=== D-klopný obvod: === | |||
[[Obrázok:D-klopny_obvodríklad.jpg]] | |||
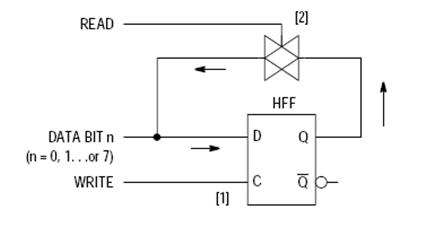
=== Bit pamäte RAM: === | |||
[[Obrázok:b_RAM.jpg]] | |||
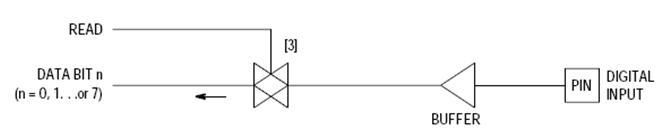
=== Bit vstupného portu: === | |||
[[Obrázok:b_IN_Port.jpg]] | |||
=== | === Bit výstupného portu: === | ||
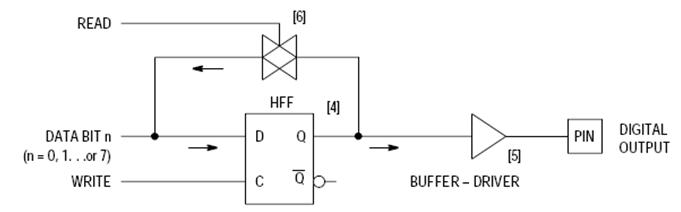
[[Obrázok:b_out_port.jpg]] | |||
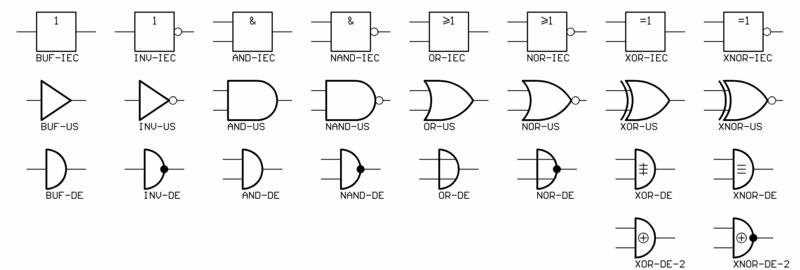
=== Značky, rôzne normy: === | |||
[[Obrázok:Znacky_obvodov.jpg]] | |||
== Číselné sústavy == | |||
Delíme ich na : | |||
* polyadické (pozičné) číselné sústavy PČS, ktoré môžeme rozvinúť do mocninového radu | |||
* nepolyadické (nepozičné)číselné sústavy NČS. Napr.: rímska číselná sústava (IX, X, XIV) | |||
=== Pozičné číselné sústavy (PČS) === | === Pozičné číselné sústavy (PČS) === | ||
| Riadok 73: | Riadok 100: | ||
kde | kde | ||
* | *<math>\ z</math> je základ pozičnej sústavy, <math>\ z \ge 2 (2, 8,{\color{red} 10}, 16)</math> | ||
Poloha číslice určuje '''rád číslice''', ktorý je definovaný '''váhou''' <math>z^{i}</math> | *<math>\ a_i</math> číslice <math>\ 0\le a_i < z</math> | ||
**ak <math>\ z</math> je prirodzené číslo, potom <math>\ a_{i}= 0,\ 1,\ ...,\ z-1</math> | |||
**Poloha číslice určuje '''rád číslice''', ktorý je definovaný '''váhou''' <math>\ v_i\ =\ z^{i}</math> | |||
* <math>\ {n-1} </math> je rád sústavy. | |||
Ak potrebujeme zapisáť racionálne číslo (väčšina) použijeme záporné mocniny až do rádu <math>k</math> | Ak potrebujeme zapisáť racionálne číslo (väčšina) použijeme záporné mocniny až do rádu <math>k</math> | ||
<math>N_z = \sum_{i=-k}^{n-1} a_i z^i</math> | <math>N_z = \sum_{i=-k}^{n-1} a_i z^i</math> | ||
| Riadok 88: | Riadok 117: | ||
Pre: | Pre: | ||
<math>z=2</math> získame dvojkovú - binárnu číselnú sústavu (0,1) | <math>\ z=2</math> získame dvojkovú - binárnu číselnú sústavu (0, 1) | ||
<math>\ z=8</math> získame osmičkovú - oktálovú číselnú sústavu (0,1,2,...,7) | |||
<math>\ z=10</math> získame desiatkovú - dekadickú číselnú sústavu (0,1,2,...,9) | |||
<math>\ z=16</math> získame šesťnástkovú - hexadecimálnu číselnú sústavu (0,1,2,...,9,A,B,C,D,E,F). Slovo ''hexadecimálny'' pochádza z gréckeho (''hexi'' - šesť) a latinského (''decem'' - desať). | |||
[[Obrázok:AP_Tab_001.jpg|thumb|250px|left]] | |||
Vlastnosti PČS: <math>N_z = \pm a_{n-1},a_{n- | |||
2}...a_{1}a_{0},a_{-1}a_{-2}...a_{-k} </math> | |||
n | |||
=== Vlastnosti PČS: === | |||
<math>N_z = \pm a_{n-1},a_{n-2}...a_{1}a_{0},a_{-1}a_{-2}...a_{-k}</math> | |||
# '''Maximálne zobraziteľné číslo:''' <math>\ N_{max} = z^{n} -z^{-k}</math> | |||
*pre celé čísla: <math>\ N_{max} = z^{n} -1</math> | |||
*pre desatinné čísla: <math>\ N_{max} = 1-z^{-k}</math> | |||
# Minimálne číslo v absolútnej hodnote rôzne od nuly: <math>\ N_{min} = z^{-k}</math> | |||
# Krok diskrétnosti: <math>\ h = z^{-k}</math> | |||
# Kapacita číselnej sústavy pre m-rádové čísla:<math>K=z^{m} =z^{n+k}</math> Pr.: z = 10, m = 3, '''K = 1000''' možných čísiel (0..999) | |||
# Počet zobrazujúcich rádov:<math>\ m = log_{z}(K+1)</math>. | |||
# Desetinná čiarka, bodka si vo všetkých číselných sústavách odpovedá. Samostatne môžeme prevádzať obe časti(celu i zlomkovú). | |||
Napríklad dekadické číslo <math>\ 2345,37_{10}</math> môžeme rozpísať do tvaru | |||
<math>\ 2345,37_{10}= 2.10^3+3.10^2 +4.10^1+5.10^0+3.10^{-1}+7.10^{-2}</math> | |||
hodnoty číslic sú | |||
<math>\ [2]_3 = 2000, [3]_2 = 300,[4]_1 = 40, [3]_{-1} = 0,3, [7]_{-2} = 0,07</math>. | |||
===?? Zobrazenie informácií v počítači ??=== | |||
Počítanie a počítače sú úzko prepojené s číslami a číselnými sústavami. V bežnom živote používame dekadické čísla (číslice '''0''', '''1''', '''2''', '''3''', '''4''', '''5''', '''6''', '''7''', '''8''', '''9''') v pozičnej číselnej sústave. Napr.: | |||
<math>\ 1234 = 1.10^3 + 2.10^2 + 3.10^1 + 4.10^0 </math> | |||
Moderné počítače vnútorne pracujú s binárnymi číslami=dvojkovými(číslice 0 a 1). | |||
Napr.: | |||
<math>\ 0_{2} = 0.2^0 = 0_{10} </math>, | |||
<math>\ 1_{2} = 1.2^0 = 1_{10} </math>, | |||
<math>\ 10_{2} = 1.2^1 + 0.2^0 = 2_{10} </math>, | |||
<math>\ 11_{2} = 1.2^1 + 1.2^0 = 3_{10} </math>, | |||
=== Pozičné číselné sústavy – prevody === | === Pozičné číselné sústavy – prevody === | ||
'''Prevod z desiatovej sústavy do číselnej sústavy so základom <math>z</math>''' : | '''Prevod z desiatovej sústavy do číselnej sústavy so základom <math>\ z</math>''' : | ||
Prevod sa vykonáva zvlášť pre | Prevod sa vykonáva zvlášť: | ||
celočíselnú časť čísla a | *pre celočíselnú časť čísla a | ||
zvlášť predesatinnú časť čísla | *zvlášť predesatinnú časť čísla | ||
'''Prevod celočíselného dekadického čísla do sústavy so základom <math>z</math> :''' | '''Prevod celočíselného dekadického čísla do sústavy so základom <math>\ z</math> :''' | ||
Metóda je založená na postupnom celočíselnom delení dekadického | Metóda je založená na postupnom celočíselnom delení dekadického | ||
'''<math>N</math>''', číslom '''<math>z</math>''',. Celočíselné delenie: | '''<math>\ N</math>''', číslom '''<math>\ z</math>''',. Celočíselné delenie: | ||
<math>\frac{M}{z}=M+R</math>, | <math>\frac{M}{z}=M+R</math>, | ||
Kde: <math>N</math> - delenec, <math>z</math> - deliteľ , <math>M</math> – podiel a <math>R</math> - zvyšok, sú celé čísla. | Kde: <math>\ N</math> - delenec, <math>\ z</math> - deliteľ , <math>\ M</math> – podiel a <math>\ R</math> - zvyšok, sú celé čísla. | ||
<math>\ (N)_z=a_{n-1}z^{n-1}+a_{n-2}z^{n-2}+...+a_{1}z+a_{0}</math> | |||
<math>(N_1)_z=\frac{(N)_z}{z} =a_{n-1}z^{n-2}+a_{n-2}z^{n-3}+...+a_{1}, \quad ((N)_z\ %\ z)=a_{0}, \quad (N)_z(mod\ z)=a_{0}</math> | |||
<math>(N_2)_z=\frac{(N_1)_z}{z} =a_{n-1}z^{n-3}+a_{n-2}z^{n-4}+...+a_{2}, \quad ((N_1)_z\ %\ z)=a_{1}</math>. | |||
Príklad: Prevod do 8-ovej sústavy: | |||
[[Obrázok:Prev_dec_okt.jpg]] | |||
Príklad: Prevod do 16-ovej sústavy: | |||
[[Obrázok:Prev_dec_hex.jpg]] | |||
Príklad: Prevod do binárnej sústay: | |||
[[Obrázok:Prev_dec_bin.jpg]] | |||
x | |||
'''Prevod z číselnej sústavy so základom <math>\ z</math> do desiatkovej sústavy :''' | |||
Vychádza zo vzťahu pre hodnotu čísla vyjadreného v danom základe číselnej sústavy ( zápis hodnoty je formálne zhodný zo zápisom čísla v dekadickej sústave) | |||
<math>\ (N)_z=a_{n-1}z^{n-1}+a_{n-2}z^{n-2}+...+a_{1}z+a_{0}</math> | |||
alebo | |||
<math>\ (N)_z=((((a_{n-1}z+a_{n-2})z+a_{n-3})z+...)z+a_{1})z+a_{0}</math> | |||
Pr. : Preveďme binárne číslo 1010111 do dekadickej sústavy | |||
'''Prvý spôsob''': | |||
<math>\ (1010111)_2=1*2^6\ +\ 0*2^5\ +\ 1*2^4\ +\ 0*2^3\ +\ 1*2^2\ +\ 1*2^1\ +\ 1*2^0\ =\ 1*64\ +\ 0*32\ +\ 1*16\ +\ 0*8\ +\ 1*4\ +\ 1*2\ +\ 1*1\ =\ 87_{10}</math> | |||
'''Druhý spôsob''': | |||
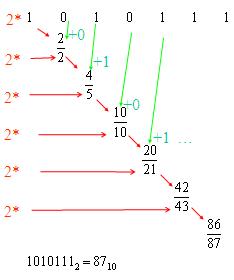
[[Obrázok:AP_Prevody_005.jpg]] | |||
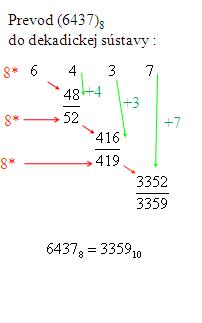
<math> | Pr.: Prevod čísla <math>\ (6437)_8</math> do dekadickej sústavy: | ||
[[Obrázok:Prev_okt_dec.jpg]] | |||
== Prevod z číselnej sústavy so základom <math>\ z</math> do číselnej sústavy so základom <math>\ w</math> : == | |||
Pri prevode zo sústavy so základom <math>\ z</math> do číselnej sústavy so základom <math>\ w</math> sa všeobecne používa schéma | |||
<math>\ N_z\ =\ (N_1)_{10}\ =\ (N_2)_{10}</math> | |||
Výnimkou sú prevody medzi sústavami pri základe <math>\ z\ =\ 2^n</math> | |||
Prevod z binárnej sústavy do oktálnej alebo hexadecimálnej sa vykoná tak, že sa binárne znaky rozdelia „odzadu“ na trojíc alebo štvoríc, a skupiny sa kódujú osobitne: | |||
Prevod binárneho čísla <math>011\ 0100\ 0111_2</math> do osmičkovej (oktálnej) sústavy: | |||
{| | |||
| rozdelíme na trojice binárnych číslic: || <math>011\ |010 |000\ |111</math> | |||
|- | |||
| vytvoríme kódy oktálnych číslic: || <math>\ 1\ |5\ |0\ |7\ </math> | |||
|- | |||
| zapíšeme výsledok: || <math>011\ 0100\ 0111_2\ = (1507)_8</math> | |||
|} | |||
Prevod binárneho čísla <math>011\ 0100\ 0111_2</math> do hexadecimálnej sústavy: | |||
*rozdelíme na štvorice binárnych číslic: <math>0011\ |0100\ |0111</math> | |||
*vytvoríme kódy hexadecimálnych číslic:<math>\ 3\ |4\ |7\ </math> | |||
*zapíšeme výsledok:<math>011\ 0100\ 0111_2\ = (347)_{16}</math> | |||
== Prevod desatinnej časti dekadického čísla do sústavy so základom <math>\ z</math> : == | |||
Metóda je založená na postupnom násobení desatinnej časti dekadického <math>\ N</math> číslom <math>\ z</math>. | |||
<math>D*z\ =\ M\ +\ D</math> | |||
kde:<math>|D|<\ 1,\qquad |D_1|<\ 1</math> a <math>\ M</math> je celé číslo. | |||
<math>(N)_z\ =\ a_{-1}z^{-1}\ +\ a_{-2}z^{-2}+\ ...\ +\ a_{-k}z^{-k}</math> | |||
<math>(N)_z*z\ =\ a_{-1}\ +\ (N_1)_z \qquad |(N)_z|< 1</math> | |||
kde: <math>\ a_{-1}</math> je celé číslo a <math>(N_1)_z\ <\ 1</math> | |||
<math>(N_1)_z*z\ =\ a_{-2}\ +\ (N_2)_z </math> | |||
kde: <math>\ a_{-2}</math> je celé číslo a <math>(N_2)_z\ <\ 1</math>, atď. | |||
Príklady: | |||
Pr.:1. Preveďme číslo <math>\ 0,12_{10}</math> do osmičkovej sústavy: | |||
[[Obrázok:Prev_db_dec_okt.jpg]] | |||
Pr.:2. Preveďme číslo <math>\ 0,6875_{10}</math> do dvojkovej sústavy: | |||
[[Obrázok:Prev_db_dec_bin.jpg]] | |||
Pr.:3. Preveďme číslo <math>\ 0,1_{10}</math> do dvojkovej sústavy: | |||
[[Obrázok:Prev_db1_dec_bin.jpg]] | |||
Číslo <math>\ 0,1_{10}</math> sa nedá vyjadriť konečným počtom binárnych číslic !! | |||
== Nepozičné číselné sústavy: == | == Nepozičné číselné sústavy: == | ||
| Riadok 170: | Riadok 339: | ||
Príklad: Číslo <math>(250)_{10}</math> zobrazené v rímskej číselnej sústave je zapísané ako číslo '''CCXV''', kde jednotlivé znaky odpovedajú hodnotám <math>[(C)]_3 = 100, [(C)]_2 = 100,[(X)]_1 = 10, [(V)]_0 = 5</math>. | Príklad: Číslo <math>(250)_{10}</math> zobrazené v rímskej číselnej sústave je zapísané ako číslo '''CCXV''', kde jednotlivé znaky odpovedajú hodnotám <math>[(C)]_3 = 100, [(C)]_2 = 100,[(X)]_1 = 10, [(V)]_0 = 5</math>. | ||
== Predhistória == | |||
Počítanie a počítače sú úzko prepojené s číslami a číselnými sústavami. Donedávna sa v Európe používali rímske číslice. Napr. číselná sústava používaná v Babylone (1900 to 180 | |||
<font style="color:green;background-color:#ffffcc;"> | |||
* 1969 - first computer networks | |||
* 1970 – UNIX | |||
* 1971 - First true microprocessor (Intel) | |||
* 1965 Objavená bola aj myš, ale začala sa používať až 1985. | |||
</font> | |||
<font color=orange style="color:green;background-color:#ffffcc;"> | |||
Vlož tabuľku. | |||
</font> | |||
Aktuálna revízia z 20:42, 21. február 2009
Základné stavebné prvky počítača
Počítač na spodnej úrovni pracuje ako elektronické zariadenie vytvorené z tranzistorov.
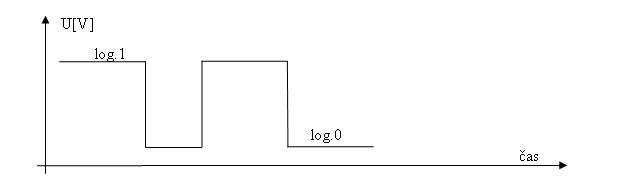
Základný režim činnosti tranzistora je: Spínací režim. Tento môžeme z fyzikálnej podstaty popísať ako: Tranzistor prúd vedie, resp. nevedie. Jednotlivým stavom tranzistora môžeme priradiť logické úrovne odpovedajúce dvojkovej číslici (bit), označené ako log.0 a log.1.
Tranzistor
Je všeobecné známe, že základom integrovaných obvodov je tranzistor. Podľa typu nosiča náboja ich delíme na:
- bipolárne (dva typy nosiča - elektróny a diery) a
- unipolárne (jeden typ nosiča).
Unipolárna technológia výroby: Sú to vlastne elektrickým poľom riadené tranzistory (FET – Field Effect Transistor).
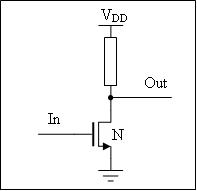
Historicky najstaršou technológiou je PMOS (Metal Oxid Semiconductor), ktorá používa unipolárny tranzistor s kanálom P. Vzhľadom na nízku rýchlosť a zlú zlučiteľnosť s TTL obvodmi sa nahradila technológiou NMOS (MOS tranzistor s kanálom N). Dosahuje vyššie rýchlosti, pretože elektróny sa pohybujú rýchlejšie ako diery. Výhodou je aj dobrá zlučiteľnosť s obvodmi TTL. Hradlo typu NMOS v invertujúcom zapojení používa ako záťaž spínacieho prvku rezistor. Hradlo NMOS zapojené ako invertor používa rezistor vo funkcii záťaže spínacieho obvodu.
xxxxxxxxxxx Výhody:
- minimalizované straty
- zlučiteľné s TTL
xxxxxxxxxxx
Technológie CMOS (Complemntary MOS)
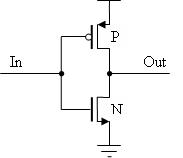
Dnes sa presadzujú technológie, v ktorých je rezistor nahradený „aktívnou“ záťažou - tranzistorom PMOS. Výhodou tejto technológie je eliminovanie stratového výkonu v statickom režime, kedy je jeden tranzistor vždy zatvorený. Tento obrázok je základom technológie CMOS (Complemntary Metal – Oxid Semiconductor). V tejto technológii Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ log.0} odpovedá napätie napätie Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ 0V} až Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0\ 0,3V_{DD}} a Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ log.1} napätie Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ 0,7V_{DD} až } Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ V_{DD}} . Pre napájacie napätie Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ V_{DD}\ =\ 5,0V} , odpovedajúce napájaniu TTL obvodov, sú rozsahy nasledovné: Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ log.0\ =\ 0V} až Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ 1,5V} a Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ log.1\ =\ 3,5V} až Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ 5.0V } .
Okrem Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ V_{DD}=5.0V} sa používa aj Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ V_{DD}=3.3V} a Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ V_{DD}=2.9V}
V ďalšom budeme uvažovať N a P MOS tranzistory ako jednoduché spínače. Napájacie napätie je unipolárne: Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ V_{DD}} .
N-typ tranzistora má vývod S pripojený na ZEM. Aby bol tranzistor vodivý – ON musí byť napätie Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ U_{GS}} voči bodu S kladné. Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ U_{GS}} musí byť väčšie ako je minimálna prahová hodnota. Napr.: Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ U_{GS}\ = \ V_{DD}} . Prechod DS je potom vodivý. Ak je napätie Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ U_{GS}\ =\ 0V} , potom je tranzistor nevodivý – v stave OFF.
P-typ tranzistora má bod S pripojený na Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ V_{DD}} . Ak má byť tranzistor v stave ON, musí byť napätie Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ U_{GS}} voči bodu S záporné. Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ U_{GS}} musí byť menšie ako je minimálna prahová hodnota. Napr.:Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ U_{GS}\ =\ 0V} . Ak je napätie Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ U_{GS}\ = \ V_{DD}} , potom je tranzistor nevodivý – v stave OFF.
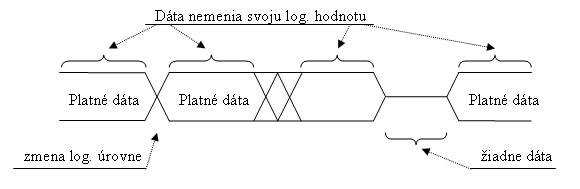
Logické úrovne – “ napätie“
Zapojenie výstupov IC
TTL obvody: logické úrovne
Základné stavebné prvky počítačov sú vytvorené :
Invertor:
NAND:
Spínač:
Trojstavový budič:
D-klopný obvod:
Bit pamäte RAM:
Bit vstupného portu:
Bit výstupného portu:
Značky, rôzne normy:
Číselné sústavy
Delíme ich na :
- polyadické (pozičné) číselné sústavy PČS, ktoré môžeme rozvinúť do mocninového radu
- nepolyadické (nepozičné)číselné sústavy NČS. Napr.: rímska číselná sústava (IX, X, XIV)
Pozičné číselné sústavy (PČS)
Hodnotu celého nezáporného čísla Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_z} vyjadríme v tvare polynómu:
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_z = \sum_{i=0}^{n-1} a_i z^i} ,
kde
- Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ z} je základ pozičnej sústavy,
- Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ a_i}
číslice Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ 0\le a_i < z}
- ak Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ z} je prirodzené číslo, potom Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ a_{i}= 0,\ 1,\ ...,\ z-1}
- Poloha číslice určuje rád číslice, ktorý je definovaný váhou Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ v_i\ =\ z^{i}}
- Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ {n-1} } je rád sústavy.
Ak potrebujeme zapisáť racionálne číslo (väčšina) použijeme záporné mocniny až do rádu Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k}
Bežne používame skrátený zápis racionálneho čísla Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_z = \pm a_{n-1},a_{n- 2}...a_{1}a_{0},a_{-1}a_{-2}...a_{-k} }
Poznámka: Rozšírenie na záporné čísla použitím znamienka mínus (-) pred číslom a používanie desatinnej čiarky je vhodné pre ľudí. V žiadnom prípade to nie je vhodný zápis pre počítač.
Pre:
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ z=2} získame dvojkovú - binárnu číselnú sústavu (0, 1)
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ z=8} získame osmičkovú - oktálovú číselnú sústavu (0,1,2,...,7)
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ z=10} získame desiatkovú - dekadickú číselnú sústavu (0,1,2,...,9)
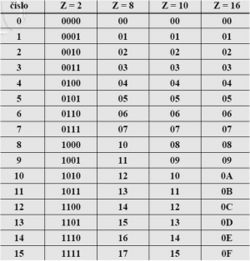
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ z=16} získame šesťnástkovú - hexadecimálnu číselnú sústavu (0,1,2,...,9,A,B,C,D,E,F). Slovo hexadecimálny pochádza z gréckeho (hexi - šesť) a latinského (decem - desať).
n
Vlastnosti PČS:
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_z = \pm a_{n-1},a_{n-2}...a_{1}a_{0},a_{-1}a_{-2}...a_{-k}}
- Maximálne zobraziteľné číslo: Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ N_{max} = z^{n} -z^{-k}}
- pre celé čísla:
- pre desatinné čísla: Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ N_{max} = 1-z^{-k}}
- Minimálne číslo v absolútnej hodnote rôzne od nuly: Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ N_{min} = z^{-k}}
- Krok diskrétnosti: Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ h = z^{-k}}
- Kapacita číselnej sústavy pre m-rádové čísla:Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K=z^{m} =z^{n+k}} Pr.: z = 10, m = 3, K = 1000 možných čísiel (0..999)
- Počet zobrazujúcich rádov:Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ m = log_{z}(K+1)} .
- Desetinná čiarka, bodka si vo všetkých číselných sústavách odpovedá. Samostatne môžeme prevádzať obe časti(celu i zlomkovú).
Napríklad dekadické číslo Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ 2345,37_{10}} môžeme rozpísať do tvaru
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ 2345,37_{10}= 2.10^3+3.10^2 +4.10^1+5.10^0+3.10^{-1}+7.10^{-2}} hodnoty číslic sú .
?? Zobrazenie informácií v počítači ??
Počítanie a počítače sú úzko prepojené s číslami a číselnými sústavami. V bežnom živote používame dekadické čísla (číslice 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) v pozičnej číselnej sústave. Napr.: Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ 1234 = 1.10^3 + 2.10^2 + 3.10^1 + 4.10^0 } Moderné počítače vnútorne pracujú s binárnymi číslami=dvojkovými(číslice 0 a 1). Napr.:
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ 0_{2} = 0.2^0 = 0_{10} } ,
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ 1_{2} = 1.2^0 = 1_{10} } ,
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ 10_{2} = 1.2^1 + 0.2^0 = 2_{10} } ,
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ 11_{2} = 1.2^1 + 1.2^0 = 3_{10} } ,
Pozičné číselné sústavy – prevody
Prevod z desiatovej sústavy do číselnej sústavy so základom Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ z} :
Prevod sa vykonáva zvlášť:
- pre celočíselnú časť čísla a
- zvlášť predesatinnú časť čísla
Prevod celočíselného dekadického čísla do sústavy so základom Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ z} :
Metóda je založená na postupnom celočíselnom delení dekadického , číslom Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ z} ,. Celočíselné delenie:
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{M}{z}=M+R} ,
Kde: Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ N} - delenec, - deliteľ , Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ M} – podiel a Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ R} - zvyšok, sú celé čísla.
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ (N)_z=a_{n-1}z^{n-1}+a_{n-2}z^{n-2}+...+a_{1}z+a_{0}}
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (N_1)_z=\frac{(N)_z}{z} =a_{n-1}z^{n-2}+a_{n-2}z^{n-3}+...+a_{1}, \quad ((N)_z\ %\ z)=a_{0}, \quad (N)_z(mod\ z)=a_{0}}
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (N_2)_z=\frac{(N_1)_z}{z} =a_{n-1}z^{n-3}+a_{n-2}z^{n-4}+...+a_{2}, \quad ((N_1)_z\ %\ z)=a_{1}} .
Príklad: Prevod do 8-ovej sústavy:
Príklad: Prevod do 16-ovej sústavy:
Príklad: Prevod do binárnej sústay:
x Prevod z číselnej sústavy so základom Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ z} do desiatkovej sústavy : Vychádza zo vzťahu pre hodnotu čísla vyjadreného v danom základe číselnej sústavy ( zápis hodnoty je formálne zhodný zo zápisom čísla v dekadickej sústave) Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ (N)_z=a_{n-1}z^{n-1}+a_{n-2}z^{n-2}+...+a_{1}z+a_{0}}
alebo
Pr. : Preveďme binárne číslo 1010111 do dekadickej sústavy
Prvý spôsob:
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ (1010111)_2=1*2^6\ +\ 0*2^5\ +\ 1*2^4\ +\ 0*2^3\ +\ 1*2^2\ +\ 1*2^1\ +\ 1*2^0\ =\ 1*64\ +\ 0*32\ +\ 1*16\ +\ 0*8\ +\ 1*4\ +\ 1*2\ +\ 1*1\ =\ 87_{10}}
Druhý spôsob:
Pr.: Prevod čísla Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ (6437)_8} do dekadickej sústavy:
Prevod z číselnej sústavy so základom Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ z} do číselnej sústavy so základom Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ w} :
Pri prevode zo sústavy so základom Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ z} do číselnej sústavy so základom Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ w} sa všeobecne používa schéma
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ N_z\ =\ (N_1)_{10}\ =\ (N_2)_{10}}
Výnimkou sú prevody medzi sústavami pri základe Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ z\ =\ 2^n}
Prevod z binárnej sústavy do oktálnej alebo hexadecimálnej sa vykoná tak, že sa binárne znaky rozdelia „odzadu“ na trojíc alebo štvoríc, a skupiny sa kódujú osobitne:
Prevod binárneho čísla Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 011\ 0100\ 0111_2}
do osmičkovej (oktálnej) sústavy:
| rozdelíme na trojice binárnych číslic: | Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 011\ |010 |000\ |111} |
| vytvoríme kódy oktálnych číslic: | Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ 1\ |5\ |0\ |7\ } |
| zapíšeme výsledok: | Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 011\ 0100\ 0111_2\ = (1507)_8} |
Prevod binárneho čísla do hexadecimálnej sústavy:
- rozdelíme na štvorice binárnych číslic: Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0011\ |0100\ |0111}
- vytvoríme kódy hexadecimálnych číslic:Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ 3\ |4\ |7\ }
- zapíšeme výsledok:Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 011\ 0100\ 0111_2\ = (347)_{16}}
Prevod desatinnej časti dekadického čísla do sústavy so základom :
Metóda je založená na postupnom násobení desatinnej časti dekadického Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ N} číslom Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ z} .
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle D*z\ =\ M\ +\ D}
kde: a Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ M} je celé číslo.
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (N)_z\ =\ a_{-1}z^{-1}\ +\ a_{-2}z^{-2}+\ ...\ +\ a_{-k}z^{-k}}
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (N)_z*z\ =\ a_{-1}\ +\ (N_1)_z \qquad |(N)_z|< 1}
kde: je celé číslo a Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (N_1)_z\ <\ 1}
Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (N_1)_z*z\ =\ a_{-2}\ +\ (N_2)_z }
kde: Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ a_{-2}} je celé číslo a , atď.
Príklady:
Pr.:1. Preveďme číslo Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ 0,12_{10}} do osmičkovej sústavy:
Pr.:2. Preveďme číslo Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ 0,6875_{10}} do dvojkovej sústavy:
Pr.:3. Preveďme číslo Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ 0,1_{10}}
do dvojkovej sústavy:
Číslo sa nedá vyjadriť konečným počtom binárnych číslic !!
Nepozičné číselné sústavy:
V nepozičných číselných sústavách vždy neplatí: Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle [a_i]_i = (a_i)z^i} .
Rímska číselná sústava (najznámejšia nepolyadická sústava).
Skladá sa zo 7 symbolov: I V X L C D M.
I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000.
Zápis: Sprava doľava. Výnimka: Ak zapíšeme číslice I, X, C pred väčšiu číslicu, potom menšiu od väčšej odčítame.
Napr: MMXMIV = 1000 + 1000 + (1000 - 10) + (5 - 1) = 2994
Číslice V, L, D môžu byť zapísané len raz a číslice I, X, C najviac trikrát za sebou. M sa môže opakovať ľubovoľne krát.
Príklad: Číslo Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (250)_{10}} zobrazené v rímskej číselnej sústave je zapísané ako číslo CCXV, kde jednotlivé znaky odpovedajú hodnotám Syntaktická analýza (parsing) neúspešná (MathML s fallbackom na SVG alebo PNG (odporúčané pre moderné prehliadače a nástroje pre zjednodušenie prístupu): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle [(C)]_3 = 100, [(C)]_2 = 100,[(X)]_1 = 10, [(V)]_0 = 5} .
Predhistória
Počítanie a počítače sú úzko prepojené s číslami a číselnými sústavami. Donedávna sa v Európe používali rímske číslice. Napr. číselná sústava používaná v Babylone (1900 to 180
- 1969 - first computer networks
- 1970 – UNIX
- 1971 - First true microprocessor (Intel)
- 1965 Objavená bola aj myš, ale začala sa používať až 1985.
Vlož tabuľku.



![{\displaystyle \ [2]_{3}=2000,[3]_{2}=300,[4]_{1}=40,[3]_{-1}=0,3,[7]_{-2}=0,07}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dde1d80588dc8aa8fa6bf7a6bad2723272f147a0)