Meranie s GPS: Rozdiel medzi revíziami
Zo stránky SensorWiki
Bez shrnutí editace |
|||
| (7 medziľahlých úprav od rovnakého používateľa nie je zobrazených.) | |||
| Riadok 13: | Riadok 13: | ||
b) aká je dynamická presnosť vašeho GPS. Prejdete 3x peši (behom) štvorec o hrane 250 m alebo 3x autom štvorec o hrane min. 1km | b) aká je dynamická presnosť vašeho GPS. Prejdete 3x peši (behom) štvorec o hrane 250 m alebo 3x autom štvorec o hrane min. 1km | ||
Výsledky zakreslíte do grafu. Aká je maximálna odchýlka medzi jednotlivými trasami? Aká je maximálna odchýlka v rohoch štvorca? | Výsledky zakreslíte do grafu. Aká je maximálna odchýlka medzi jednotlivými trasami? Aká je maximálna odchýlka v rohoch štvorca? Ak budete pracovať vo dvojici, treba prejsť štvorec 2x jedným a 2x opačným smerom. | ||
Zoberte do úvahy aj presnosť pohybu - prešli ste skutočne cez rovnaké miesta? Označte si napríklad rohy štvorca nejakou dočasnou značkou. | |||
Meranie nemusíte robiť v reálnom čase, t.j. môžete si data zaznamenať, napr. do súboru a výpočty robiť potom neskôr. | Meranie nemusíte robiť v reálnom čase, t.j. môžete si data zaznamenať, napr. do súboru a výpočty robiť potom neskôr. | ||
Ak vám nevychádza štvorec, môže to byť aj iný vhodný mnohouholník, aj nepravidelný. Rozmery sú takisto len odporúčané. | |||
| Riadok 26: | Riadok 27: | ||
[[Súbor:GPSprecisionImage.png|x300px]] [[Súbor:GPSprecisionSquareImage.png|x300px]] | |||
'''Tipy:''' | '''Tipy:''' | ||
| Riadok 36: | Riadok 35: | ||
Môže sa vám hodiť: | Môže sa vám hodiť: | ||
* Konvertor GPX do CSV (lebo .csv viete otvoriť v Exceli) | * Konvertor GPX do CSV (lebo .csv viete otvoriť v Exceli) https://www.gpsvisualizer.com/convert_input | ||
* Výpočet vzdialeností z Lat/Lon súradníc | * Výpočet vzdialeností z Lat/Lon súradníc https://www.movable-type.co.uk/scripts/latlong.html | ||
* Using Processing to read GPS data and displaying a map https://www.dfrobot.com/blog-198.html | |||
Na dlhšie čítanie: | |||
* GPS Accuracy. Tools & Tips to Test Your Device https://lembergsolutions.com/blog/gps-accuracy-tools-tips-test-your-device | |||
* https://www.researchgate.net/post/Using_a_phone_as_scientific_GPS_how_accurate_technical_specifications_Apps | |||
* https://debrief.github.io/? - marine analysis? | |||
Utilitky pre váš telefón: | |||
* https://play.google.com/store/apps/details?id=precise.GPS.v2.free&hl=en_US | |||
* https://play.google.com/store/apps/details?id=com.chartcross.gpstest&hl=en_US | |||
| Riadok 59: | Riadok 71: | ||
\,\!</math> | \,\!</math> | ||
Znamienko výsledku je v ďalších výpočtoch nepodstatné. | |||
" | "Priemerná šírka" sa vypočíta takto: | ||
:<math>\phi_m=\frac{\phi_1+\phi_2}{2}.\,\!</math> | :<math>\phi_m=\frac{\phi_1+\phi_2}{2}.\,\!</math> | ||
Colatitude | Veličina ''Colatitude'' sa vypočíta takto: | ||
: | :Pre šírky vyjadrené v radiánoch: | ||
::<math>\theta=\frac{\pi}{2}-\phi;\,\!</math> | ::<math>\theta=\frac{\pi}{2}-\phi;\,\!</math> | ||
: | :v stupňoch: | ||
::<math>\theta=90^\circ-\phi.\,\!</math> | ::<math>\theta=90^\circ-\phi.\,\!</math> | ||
Pre naše výpočty budeme uvažovať polomer Zeme | |||
:<math>R\,\!</math> = 6, | :<math>R\,\!</math> = 6 371,009 km | ||
<math>D_\,\!</math> = | <math>D_\,\!</math> = vzdialenosť medzi dvoma bodmi meraná na povrchu Zeme (resp. jej idealizovaného modelu). Výsledok je v rovnakých jednotkách | ||
ako polomer R (teda km). | |||
== | |||
==Výpočet pre Plochozem == | |||
Podľa https://en.wikipedia.org/wiki/Geographical_distance | Podľa https://en.wikipedia.org/wiki/Geographical_distance | ||
Na malých vzdialenostiach nám postačí aproximovať povrch Zeme rovinou. Pre väčšie vzdialenosti chyba výpočtu rastie, podobne ak je bod bližšie | |||
ku geografickým pólom. | |||
Najkratšia vzdialenosť medzi dvoma bodmi v rovine je rovná čiara. Na výpočet jej dĺžky postačí Pytagorova veta. Presnosť výpočtu však závisí aj | |||
tak od projekcii súradníc do roviny, čo je v podstate hlavný problém, ktorým sa zaoberá kartografia. | |||
=== Sférická Zem premietnutá do roviny === | |||
Nasledujúci vzťah berie do úvahy zmeny vzdialenosti medzi poludníkmi v závislosti od zemepisnej šírky: | |||
=== | :<math>D=R\sqrt{(\Delta\phi)^2+(\cos(\phi_m)\Delta\lambda)^2},</math> | ||
:kde: | |||
::<math>\Delta\phi\,\!</math> a <math>\Delta\lambda\,\!</math> sú v radiánoch, | |||
::<math>\phi_m\,\!</math> musí byť v jednotkách vhodných pre výpočet <math>\cos(\phi_m).\,\!</math> | |||
Táto aproximácia je veľmi jednoduchá a rýchla a dáva vcelku dobré výsledky pre malé vzdialenosti. Je vhodná napríklad | |||
tam, kde potrebujeme usporiadať meranie podľa vzdialenosti (tam nám dokonca stačí použiť štvorec vzdialenosti a vyhneme | |||
sa počítaniu odmocniny). | |||
Tento algoritmus (haversin formula) je už trocha zložitejší (pozri https://www.movable-type.co.uk/scripts/latlong.html): | |||
<source lang="cpp"> | |||
float distanceInKmBetweenEarthCoordinates(float lat1, float lon1, float lat2, float lon2) | |||
{ | |||
var earthRadiusKm = 6371; | |||
var dLat = radians(lat2-lat1); | |||
var dLon = radians(lon2-lon1); | |||
lat1 = radians(lat1); | |||
lat2 = radians(lat2); | |||
float a = sin(dLat/2) * sin(dLat/2) + | |||
: | sin(dLon/2) * sin(dLon/2) * cos(lat1) * cos(lat2); | ||
float c = 2 * atan2( sqrt(a), sqrt(1-a)); | |||
return earthRadiusKm * c; | |||
} | |||
Source: https://stackoverflow.com/questions/365826/calculate-distance-between-2-gps-coordinates | |||
</source> | |||
Implementácia vyššieuvedených vzťahov je predvedená v tejto ukážke, ktorá vypočíta | |||
vzdialenosť dvoch bodov. Poznámka: Processing očakáva pre goniometrické funkcie sin() a spol. hodnotu argumentu v radianoch! | |||
Využívame preto fuknciu radians(degrees); ktorá prevedie stupne na radiány. | |||
*/ | |||
<source lang="cpp"> | |||
/* Malacky */ | |||
float lat1 = radians(48.4406503); | |||
float lon1 = radians(17.0245442); | |||
/* Rohožník */ | |||
float lat2 = radians(48.4628517); // stupnov | |||
float lon2 = radians(17.1625600); // stupnov | |||
float Rz = 6371.009; // km | |||
void setup() | |||
{ | |||
size(400, 400); | |||
float dLat = lat1 - lat2; | |||
float dLon = lon1 - lon2; | |||
float mLat = (lat1 + lat2)/2; | |||
float col1 = 90.0 - lat1; | |||
float col2 = 90.0 - lat2; | |||
float Distance = 0.0; | |||
Distance = Rz*sqrt( sq(dLat) + sq(cos(mLat)*dLon) ); | |||
println(" Flat Earth distance: " + Distance + " km"); | |||
float a = sin(dLat/2) * sin(dLat/2) + | |||
sin(dLon/2) * sin(dLon/2) * cos(lat1) * cos(lat2); | |||
float c = 2 * atan2(sqrt(a), sqrt(1-a)); | |||
Distance = Rz * c; | |||
println("Spherical Earth distance: " + Distance + " km"); | |||
} | } | ||
void draw() { /* nekresli nic tentoraz */ } | |||
</source> | </source> | ||
Dá takýto výsledok | |||
Flat Earth distance: 10.473797 km | |||
Spherical Earth distance: 10.473796 km | |||
Rohoznik - Malacky je 10.38 km podla mapy.cz | |||
[[MEMS inteligentné senzory a aktuátory#Cvi.C4.8Denia|Návrat na zoznam cvičení...]] | [[MEMS inteligentné senzory a aktuátory#Cvi.C4.8Denia|Návrat na zoznam cvičení...]] | ||
[[Category:MEMS]] | [[Category:MEMS]] | ||
Aktuálna revízia z 08:55, 30. marec 2021
Modifikované cvičenie na DOMA:
Úloha:
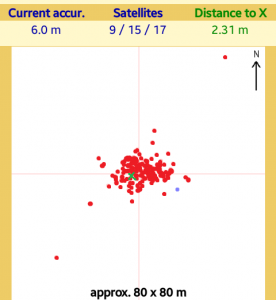
Spravte základné testovanie presnosti GPS snímačov.
Zistite:
a) aká je statická presnosť vašeho GPS. Meranie v jednom bode vykonávajte nepretržite minimálne 6 hodín (napr. v noci) a získané údaje zakreslite do X-Y grafu. Určite aká je maximálna odchýlka, max. priemerná odchýlka a max. odchýlka priemeru od správnej hodnoty (ak sa vám podarí ju získať). Minimálny počet bodov je 36 (6x6). Ak budete pracovať vo dvojici, počet bodov je dvojnásobný.
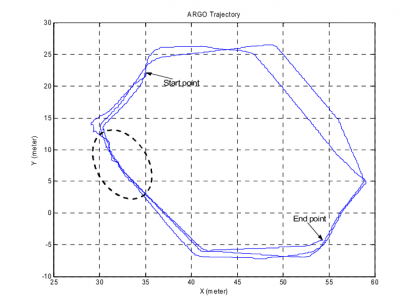
b) aká je dynamická presnosť vašeho GPS. Prejdete 3x peši (behom) štvorec o hrane 250 m alebo 3x autom štvorec o hrane min. 1km
Výsledky zakreslíte do grafu. Aká je maximálna odchýlka medzi jednotlivými trasami? Aká je maximálna odchýlka v rohoch štvorca? Ak budete pracovať vo dvojici, treba prejsť štvorec 2x jedným a 2x opačným smerom.
Zoberte do úvahy aj presnosť pohybu - prešli ste skutočne cez rovnaké miesta? Označte si napríklad rohy štvorca nejakou dočasnou značkou.
Meranie nemusíte robiť v reálnom čase, t.j. môžete si data zaznamenať, napr. do súboru a výpočty robiť potom neskôr. Ak vám nevychádza štvorec, môže to byť aj iný vhodný mnohouholník, aj nepravidelný. Rozmery sú takisto len odporúčané.
Odovzdať treba:
- video na ktorom vidno ako experiment prebiehal
- grafické zobrazenie trajektórie v mape (mapy.cz, strava.com a pod.)
- referát s výpočtami a vyhodnotením presnosti
- ak ste použili vlastný softvér, tak zdrojáky (.pde alebo .m a pod.)
Tipy:
Môže sa vám hodiť:
- Konvertor GPX do CSV (lebo .csv viete otvoriť v Exceli) https://www.gpsvisualizer.com/convert_input
- Výpočet vzdialeností z Lat/Lon súradníc https://www.movable-type.co.uk/scripts/latlong.html
- Using Processing to read GPS data and displaying a map https://www.dfrobot.com/blog-198.html
Na dlhšie čítanie:
- GPS Accuracy. Tools & Tips to Test Your Device https://lembergsolutions.com/blog/gps-accuracy-tools-tips-test-your-device
- https://www.researchgate.net/post/Using_a_phone_as_scientific_GPS_how_accurate_technical_specifications_Apps
- https://debrief.github.io/? - marine analysis?
Utilitky pre váš telefón:
- https://play.google.com/store/apps/details?id=precise.GPS.v2.free&hl=en_US
- https://play.google.com/store/apps/details?id=com.chartcross.gpstest&hl=en_US
Definície a označenie
Budeme počítať vzdialenosť medzi dvoma bodmi a . Zemepisné súradnice sú dané zemepisnou šírkou a zemepisnou dĺžkou (latitude, longitude) oboch bodov a . Na ich poradí pre účely výpočtu vzdialenosti nezáleží.
Orientácia zemepisných súradníc je daná tak, že Sever (N) a Východ (E) sa vyjadrujú kladným, Juh (S) a Západ (W) záporným číslom. Zemepisné súradnice sa obvykle vyjadrujú v stupňoch, pri výpočte ich treba previesť do takých jednotiek, v akých očakávajú argument goniometrické funkcie na kalkulačke alebo vo vašom algoritme (stupne, radiány). Okrem toho si treba uvedomiť, že minúty a sekundy sú zo 60, takže S31 30' je -31,5 stupňa. Prevod stupňov na radiány je jednoduchý: radians = degrees * PI / 180.
function degreesToRadians(degrees) {
return degrees * PI / 180;
}
Označíme si pomocné rozdiely v súradniciach nasledovne:
Znamienko výsledku je v ďalších výpočtoch nepodstatné.
"Priemerná šírka" sa vypočíta takto:
Veličina Colatitude sa vypočíta takto:
- Pre šírky vyjadrené v radiánoch:
- v stupňoch:
Pre naše výpočty budeme uvažovať polomer Zeme
- = 6 371,009 km
= vzdialenosť medzi dvoma bodmi meraná na povrchu Zeme (resp. jej idealizovaného modelu). Výsledok je v rovnakých jednotkách ako polomer R (teda km).
Výpočet pre Plochozem
Podľa https://en.wikipedia.org/wiki/Geographical_distance
Na malých vzdialenostiach nám postačí aproximovať povrch Zeme rovinou. Pre väčšie vzdialenosti chyba výpočtu rastie, podobne ak je bod bližšie ku geografickým pólom.
Najkratšia vzdialenosť medzi dvoma bodmi v rovine je rovná čiara. Na výpočet jej dĺžky postačí Pytagorova veta. Presnosť výpočtu však závisí aj tak od projekcii súradníc do roviny, čo je v podstate hlavný problém, ktorým sa zaoberá kartografia.
Sférická Zem premietnutá do roviny
Nasledujúci vzťah berie do úvahy zmeny vzdialenosti medzi poludníkmi v závislosti od zemepisnej šírky:
- kde:
- a sú v radiánoch,
- musí byť v jednotkách vhodných pre výpočet
Táto aproximácia je veľmi jednoduchá a rýchla a dáva vcelku dobré výsledky pre malé vzdialenosti. Je vhodná napríklad tam, kde potrebujeme usporiadať meranie podľa vzdialenosti (tam nám dokonca stačí použiť štvorec vzdialenosti a vyhneme sa počítaniu odmocniny).
Tento algoritmus (haversin formula) je už trocha zložitejší (pozri https://www.movable-type.co.uk/scripts/latlong.html):
float distanceInKmBetweenEarthCoordinates(float lat1, float lon1, float lat2, float lon2)
{
var earthRadiusKm = 6371;
var dLat = radians(lat2-lat1);
var dLon = radians(lon2-lon1);
lat1 = radians(lat1);
lat2 = radians(lat2);
float a = sin(dLat/2) * sin(dLat/2) +
sin(dLon/2) * sin(dLon/2) * cos(lat1) * cos(lat2);
float c = 2 * atan2( sqrt(a), sqrt(1-a));
return earthRadiusKm * c;
}
Source: https://stackoverflow.com/questions/365826/calculate-distance-between-2-gps-coordinates
Implementácia vyššieuvedených vzťahov je predvedená v tejto ukážke, ktorá vypočíta vzdialenosť dvoch bodov. Poznámka: Processing očakáva pre goniometrické funkcie sin() a spol. hodnotu argumentu v radianoch! Využívame preto fuknciu radians(degrees); ktorá prevedie stupne na radiány.
- /
/* Malacky */
float lat1 = radians(48.4406503);
float lon1 = radians(17.0245442);
/* Rohožník */
float lat2 = radians(48.4628517); // stupnov
float lon2 = radians(17.1625600); // stupnov
float Rz = 6371.009; // km
void setup()
{
size(400, 400);
float dLat = lat1 - lat2;
float dLon = lon1 - lon2;
float mLat = (lat1 + lat2)/2;
float col1 = 90.0 - lat1;
float col2 = 90.0 - lat2;
float Distance = 0.0;
Distance = Rz*sqrt( sq(dLat) + sq(cos(mLat)*dLon) );
println(" Flat Earth distance: " + Distance + " km");
float a = sin(dLat/2) * sin(dLat/2) +
sin(dLon/2) * sin(dLon/2) * cos(lat1) * cos(lat2);
float c = 2 * atan2(sqrt(a), sqrt(1-a));
Distance = Rz * c;
println("Spherical Earth distance: " + Distance + " km");
}
void draw() { /* nekresli nic tentoraz */ }
Dá takýto výsledok
Flat Earth distance: 10.473797 km Spherical Earth distance: 10.473796 km Rohoznik - Malacky je 10.38 km podla mapy.cz



![{\displaystyle A[\phi _{1},\lambda _{1}]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16785a6dd622b5e47852b22e632d9fa0f838f2e4)
![{\displaystyle B[\phi _{2},\lambda _{2}],\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7dbee6ac585aff898a2c1daafeae9a094191f462)










