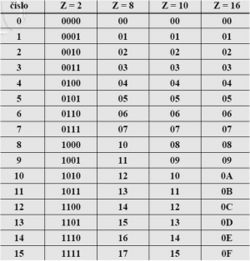
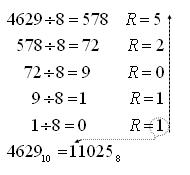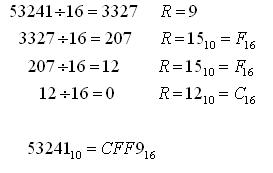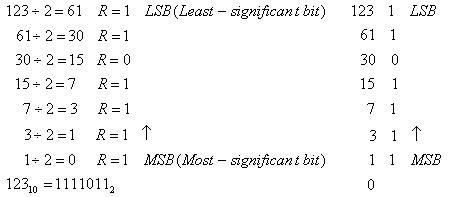Číselné sústavy
Z SensorWiki
Obsah
Číselné sústavy
Delíme ich na :
- polyadické (pozičné) číselné sústavy PČS, ktoré môžeme rozvinúť do mocninového radu
- nepolyadické (nepozičné)číselné sústavy NČS. Napr.: rímska číselná sústava (IX, X, XIV)
Pozičné číselné sústavy (PČS)
Hodnotu celého nezáporného čísla 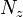 vyjadríme v tvare polynómu:
vyjadríme v tvare polynómu:
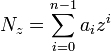 ,
,
kde
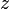 je základ pozičnej sústavy,
je základ pozičnej sústavy, 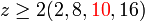
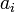 číslice
číslice 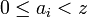
- ak
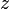 je prirodzené číslo, potom
je prirodzené číslo, potom 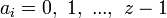
- Poloha číslice určuje rád číslice, ktorý je definovaný váhou
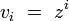
- ak
-
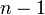 je rád sústavy.
je rád sústavy.
Ak potrebujeme zapisáť racionálne číslo (väčšina) použijeme záporné mocniny až do rádu 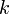
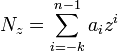
Bežne používame skrátený zápis racionálneho čísla 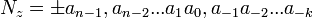
Poznámka: Rozšírenie na záporné čísla použitím znamienka mínus (-) pred číslom a používanie desatinnej čiarky je vhodné pre ľudí. V žiadnom prípade to nie je vhodný zápis pre počítač.
Pre:
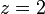 získame dvojkovú - binárnu číselnú sústavu (0, 1)
získame dvojkovú - binárnu číselnú sústavu (0, 1)
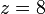 získame osmičkovú - oktálovú číselnú sústavu (0,1,2,...,7)
získame osmičkovú - oktálovú číselnú sústavu (0,1,2,...,7)
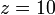 získame desiatkovú - dekadickú číselnú sústavu (0,1,2,...,9)
získame desiatkovú - dekadickú číselnú sústavu (0,1,2,...,9)
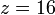 získame šesťnástkovú - hexadecimálnu číselnú sústavu (0,1,2,...,9,A,B,C,D,E,F). Slovo hexadecimálny pochádza z gréckeho (hexi - šesť) a latinského (decem - desať).
získame šesťnástkovú - hexadecimálnu číselnú sústavu (0,1,2,...,9,A,B,C,D,E,F). Slovo hexadecimálny pochádza z gréckeho (hexi - šesť) a latinského (decem - desať).
Vlastnosti PČS:
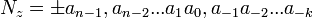
- Maximálne zobraziteľné číslo:
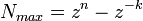
- pre celé čísla:
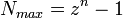
- pre desatinné čísla:
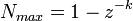
- Minimálne číslo v absolútnej hodnote rôzne od nuly:
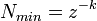
- Krok diskrétnosti:
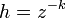
- Kapacita číselnej sústavy pre m-rádové čísla:
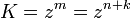 Pr.: z = 10, m = 3, K = 1000 možných čísiel (0..999)
Pr.: z = 10, m = 3, K = 1000 možných čísiel (0..999) - Počet zobrazujúcich rádov:
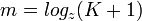 .
. - Desetinná čiarka, bodka si vo všetkých číselných sústavách odpovedá. Samostatne môžeme prevádzať obe časti(celu i zlomkovú).
Napríklad dekadické číslo 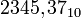 môžeme rozpísať do tvaru
môžeme rozpísať do tvaru
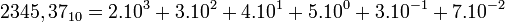 hodnoty číslic sú
hodnoty číslic sú
![\ [2]_3 = 2000, [3]_2 = 300,[4]_1 = 40, [3]_{-1} = 0,3, [7]_{-2} = 0,07](/sensorwiki/images/math/b/1/a/b1a6cd94980106c545b89a24ec9c3862.png) .
.
Zobrazenie informácií v počítači
Počítanie a počítače sú úzko prepojené s číslami a číselnými sústavami. V bežnom živote používame dekadické čísla (číslice 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) v pozičnej číselnej sústave. Napr.:
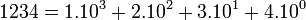
Moderné počítače vnútorne pracujú s binárnymi číslami=dvojkovými(číslice 0 a 1).
Napr.:
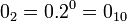 ,
,
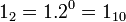 ,
,
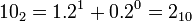 ,
,
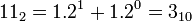 ,
,
Pozičné číselné sústavy – prevody
Prevod z desiatkovej sústavy do číselnej sústavy so základom 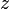 :
:
Prevod sa vykonáva zvlášť:
- pre celočíselnú časť čísla a
- zvlášť predesatinnú časť čísla
Prevod celočíselného dekadického čísla do sústavy so základom 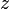 :
:
Metóda je založená na postupnom celočíselnom delení dekadického
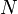 , číslom
, číslom 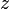 ,. Celočíselné delenie:
,. Celočíselné delenie:
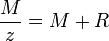 ,
,
Kde: 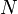 - delenec,
- delenec, 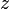 - deliteľ ,
- deliteľ , 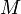 – podiel a
– podiel a 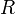 - zvyšok, sú celé čísla.
- zvyšok, sú celé čísla.
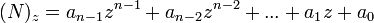
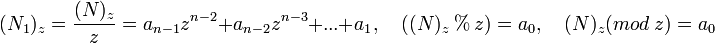
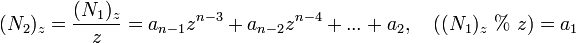 .
.
Príklad: Prevod do 8-ovej sústavy:
Príklad: Prevod do 16-ovej sústavy:
Príklad: Prevod do binárnej sústay:
Prevod z číselnej sústavy so základom 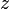 do desiatkovej sústavy :
Vychádza zo vzťahu pre hodnotu čísla vyjadreného v danom základe číselnej sústavy ( zápis hodnoty je formálne zhodný zo zápisom čísla v dekadickej sústave)
do desiatkovej sústavy :
Vychádza zo vzťahu pre hodnotu čísla vyjadreného v danom základe číselnej sústavy ( zápis hodnoty je formálne zhodný zo zápisom čísla v dekadickej sústave)
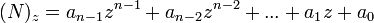
alebo
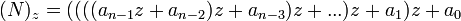
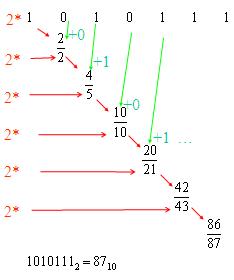
Pr. : Preveďme binárne číslo 1010111 do dekadickej sústavy
Prvý spôsob:
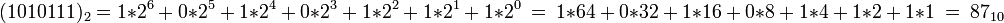
Druhý spôsob:
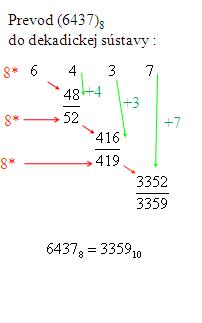
Pr.: Prevod čísla 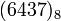 do dekadickej sústavy:
do dekadickej sústavy:
Prevod z číselnej sústavy so základom 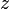 do číselnej sústavy so základom
do číselnej sústavy so základom 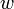 :
:
Pri prevode zo sústavy so základom 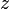 do číselnej sústavy so základom
do číselnej sústavy so základom 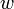 sa všeobecne používa schéma
sa všeobecne používa schéma
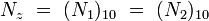
Výnimkou sú prevody medzi sústavami pri základe 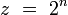
Prevod z binárnej sústavy do oktálnej alebo hexadecimálnej sa vykoná tak, že sa binárne znaky rozdelia „odzadu“ na trojíc alebo štvoríc, a skupiny sa kódujú osobitne:
Prevod binárneho čísla 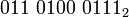 do osmičkovej (oktálnej) sústavy:
do osmičkovej (oktálnej) sústavy:
| rozdelíme na trojice binárnych číslic: | 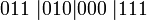
|
| vytvoríme kódy oktálnych číslic: | 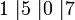
|
| zapíšeme výsledok: | 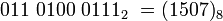
|
Prevod binárneho čísla 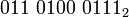 do hexadecimálnej sústavy:
do hexadecimálnej sústavy:
- rozdelíme na štvorice binárnych číslic:
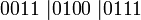
- vytvoríme kódy hexadecimálnych číslic:
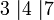
- zapíšeme výsledok:
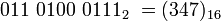
Nepozičné číselné sústavy:
V nepozičných číselných sústavách vždy neplatí: ![[a_i]_i = (a_i)z^i](/sensorwiki/images/math/0/0/e/00e85f6e7eceaf08e5e9e04b7a78e620.png) .
.
Rímska číselná sústava (najznámejšia nepolyadická sústava).
Skladá sa zo 7 symbolov: I V X L C D M.
I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000.
Zápis: Sprava doľava. Výnimka: Ak zapíšeme číslice I, X, C pred väčšiu číslicu, potom menšiu od väčšej odčítame.
Napr: MMXMIV = 1000 + 1000 + (1000 - 10) + (5 - 1) = 2994
Číslice V, L, D môžu byť zapísané len raz a číslice I, X, C najviac trikrát za sebou. M sa môže opakovať ľubovoľne krát.
Príklad: Číslo 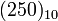 zobrazené v rímskej číselnej sústave je zapísané ako číslo CCXV, kde jednotlivé znaky odpovedajú hodnotám
zobrazené v rímskej číselnej sústave je zapísané ako číslo CCXV, kde jednotlivé znaky odpovedajú hodnotám ![[(C)]_3 = 100, [(C)]_2 = 100,[(X)]_1 = 10, [(V)]_0 = 5](/sensorwiki/images/math/5/3/1/5311aba026df8bc6d242543d007eb630.png) .
.